Authors:
(1) Jongmin Lee, Department of Mathematical Science, Seoul National University;
(2) Ernest K. Ryu, Department of Mathematical Science, Seoul National University and Interdisciplinary Program in Artificial Intelligence, Seoul National University.
1.1 Notations and preliminaries
2.1 Accelerated rate for Bellman consistency operator
2.2 Accelerated rate for Bellman optimality opera
5 Approximate Anchored Value Iteration
6 Gauss–Seidel Anchored Value Iteration
7 Conclusion, Acknowledgments and Disclosure of Funding and References
B Omitted proofs in Section 2
First, we prove the following lemma by induction.








Now, we present our key lemmas for the first rate of Theorem 2.

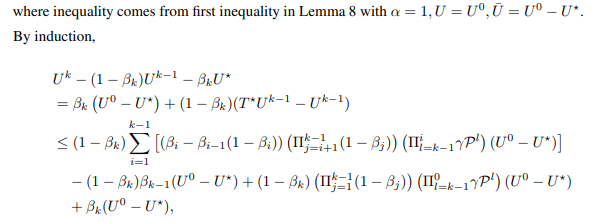
and let U¯ be the entire right hand side of inequality. Then, we have

By induction,
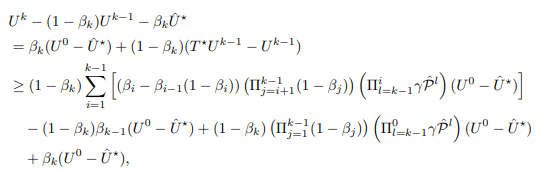
and let U¯ be the entire right hand side of inequality. Then, we have
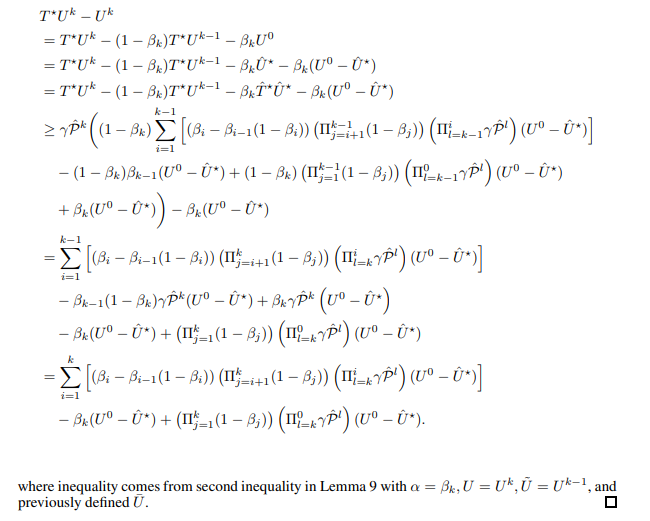
Now, we prove the first rate of Theorem 2.


where the second inequality is from the condition.
By induction,
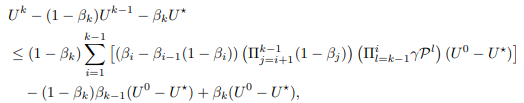
and let U¯ be the entire right hand side of inequality. Then, we have

Now, we prove the second rates of Theorem 2.

This paper is available on arxiv under CC BY 4.0 DEED license.